Sunday, May 29, 2022

Pythagorean Theorem Practice Test - Free Math Resource!

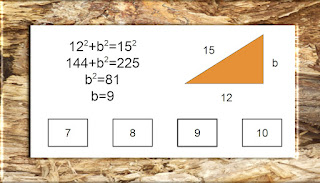
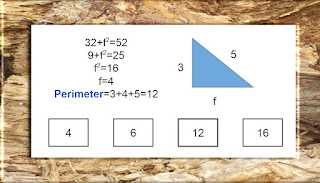
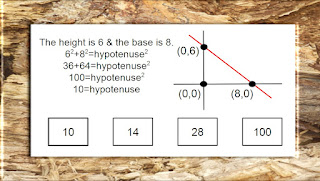
This free resource offers a practice test featuring the Pythagorean Theorem. It includes 15 questions ranging from simple to more complex questions. This practice test is created in adaptive mode so that you can check your answers immediately after each question. If you aren't familiar with this theorem or would like to review information related to it, you may wish to visit Khan Academy's Pythagorean Theorem video.

Directions

  1. Click on the first graphic to enlarge to full screen.
  2. Record your answers on a piece of paper.
  3. Click on the graphic or the next thumbnail at the bottom of the screen.
  4. Check your answers.

Thank you very much for visiting my Student Survive 2 Thrive blog! If you would like to see more of my resources, you have several options: click on my site map, go to the topics options, or type your desired topic into my search bar. Below are a few additional math resources that I have created:

Pythagorean Theorem Free Practice Test

Created by Katrena - All rights reserved

What is the value for c? The two legs of the right triangle measure 3 and 4. Choices are 2, 3, 4, or 5.

c=5 (Use the Pythagorean Theorem to determine this answer by using a squared + b squared = c squared.)

What is the value for x? Right triangle legs are 6 and 8. Choices are: 9, 10, 12, and 15.

x=10 (Use the Pythagorean Theorem in which a squared + b squared = c squared).

What is the value for b? Right triangle leg is 12 and the hypotenuse is 15. Choices are: 7, 8, 9, and 10

b=9 using the Pythagorean Theorem

What is the value for p? Right triangle leg is 4 and the hypotenuse is 5. Choices are: 3, 6, 8, and 10.

p=3 using the Pythagorean Theorem

What is the perimeter of the triangle? Right triangle has a leg of 3 and hypotenuse of 5 and an unknown variable for the other leg. Choices are: 4, 6, 12, and 16.

The perimeter equals 12. Use the Pythagorean Theorem to determine the missing variable and then add all sides.

What is the perimeter of the triangle? Right triangle pictured: one leg is 9 and the hypotenuse is 15. Choices are: 6, 12, 24, and 36.

The perimeter is 36. Use the Pythagorean Theorem to determine the missing leg and then add all 3 sides.

What is the perimeter of the rectangle? Picture includes a rectangle with a height of 3. A line is drawn diagonally from the top right to the bottom left of the rectangle and that has a length of 5. The base has an unknown variable. Choices are: 4, 12, 14, and 19.

The perimeter of the rectangle is 14. Use the Pythagorean Theorem to determine the base. Add all four numbers on the rectangle to get the perimeter.

What is the area of the triangle? Right triangle pictured with a leg of 8 and hypotenuse of 10 with an unknown variable for the other leg. Choices are: 24, 48, 28, and 6.

The area of the triangle is 24. Use the Pythagorean Theorem to determine the height. Area of a triangle = 1/2 base times the height.

What is the perimeter of the square? Pictured is a square with an unknown variable for the width and height. A line extends across the square from top left to bottom right with a length of the square root of 18. Choices are: 81, 72, 36, and 12.

The perimeter of the square is 12. Use the Pythagorean Theorem to determine that all sides of the square equal 3. Add all four sides to get 12.

What is the area of the square? A square is pictured with unknown variables for the height and width. A line extends from the top left corner to the bottom right corner with a length of the square root of 50. Choices are: 12.5, 20, 25, 625.

Area of the square is 25. Use the Pythagorean Theorem to determine that the sides of the square equal 5. Multiply the height and width to determine the area of a square.

What is the length of the hypotenuse? Pictured is a right triangle with the following coordinates: (0,6), (0,0), and (8,0). Choices are 10, 14, 28, and 100.

The length of the hypotenuse is 10. Use the Pythagorean Theorem to determine that the two legs are 6 and 8 with a resulting hypotenuse of 10.

What are the coordinates for k? A pictured graph has 3 triangle coordinates. K is above l and is unknown. L has coordinates of (0,0). M has coordinates of (8,0). Choices are: (0,10), (6,0), (12,0), (0,6).

The missing coordinates are (0,6). Use the Pythagorean Theorem to determine that the missing side has a height of 6.

What is the area of the triangle? Pictured is a graph forming a right triangle with the following coordinates: (0,12), (0,0), and (16,0). Choices are: 20, 96, 120, and 192).

The area of the triangle is 96. The base is 16 and the height is 12. Area of a triangle equals 1/2 base times the height.

Michael marked points on a graph at (8,0) and (0,6). He then drew a line through them, forming a triangle with the origin. What is the perimeter of the resulting triangle? Choices are: 24, 48, 60, and 68.

The perimeter of the triangle is 24. Use the Pythagorean Theorem to determine legs of 8 and 6 and a hypotenuse of 10.

Carlotta graphed a straight line using a linear equation of y= -4/3x+4. The line created a triangle with the point where the x- and y-axes cross over. What is the perimeter of the resulting triangle? Choices are: 5, 6, 12, and 24.

The perimeter of the triangle is 12. Use the Pythagorean Theorem to determine 2 legs of 4 and 3 with a hypoteneuse of 5. Add the 3 sides to get the perimeter.

Find more resources at StudentSurvive2Thrive.blogspot.com


Posted by at
Labels: , , , , , ,

No comments:

Post a Comment

Thanks for reading my article and sending your comment! Please note that I do not place links to other web sites on this blog.

Note: Only a member of this blog may post a comment.

Subscribe to: Post Comments (Atom)