Student Survive 2 Thrive: Horizontal Linear Equations and Graphs Including Real Life Examples

Saturday, May 28, 2022

Horizontal Linear Equations and Graphs Including Real Life Examples

This free math practice test includes examples from real life that would result in graphing points that when drawing through them would create a horizontal line. I created this practice test in adaptive mode so that you can the correct answers on the next slide along with a detailed explanation.

Directions

Click on the first graphic below.
Write your answers on paper and graph your answers on graph paper.
Click on the graphic or on the next thumbnail at the bottom of the screen to advance to the next slide.
Check your answers and review the detailed feedback if needed.
Repeat the above steps if you wish to review the information again.

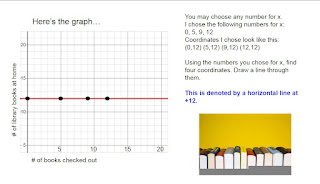
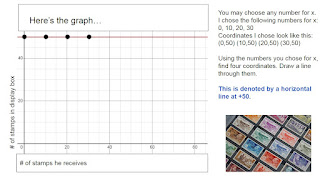
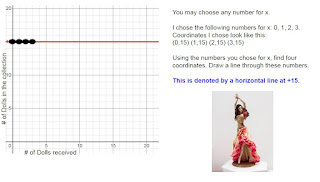
Note: In an effort to create a resource that includes real life examples, it is helpful to understand that the real life examples would in reality be specific points on a graph and would not equate to a line that would include all values for y between the numbers given. However, for the purposes of practicing this level of math, the linear equations would result from a line drawn that would connect and continue beyond these points.

I hope you enjoy my free resources on Student Survive 2 Thrive. If you wish to find more resources, you have several options: go to my site map, go to your desired topic such as math, or type your desired topic in my search bar. I've also included some related math practice tests below:

Horizontal Linear Equations & Graphs Free Practice Test

Created by Katrena - All rights reserved

Larry is at an Easter egg hunt. He currently has 7 eggs in his basket. Every time he bends over to pick up an egg, he drops the same number of eggs. When he picks up 2 eggs, he drops 2 eggs. When he picks up 3 eggs, he drops 3 eggs. The same thing happens when he picks up four eggs. Larry is frustrated when he sees that he only has 7 eggs at the end of the hunt! Create an equation in y=mx+b format and graph the equation.

The resulting graph is a horizontal line where y=7.

Chia-Hao has a toy collection with 20 toys. His dad said he can keep collecting toys, but for every toy he adds to his collection, he will have to donate or sell the same number of toys. If he adds 5, 10, or even 15 toys, Chia-Hao will donate the same number of toys. Write the equation using y=mx+b format and graph it.

The graph is a horizontal line where y=20

Zuzanna loves to go to the library. She always makes sure that she has 12 books at home to read. If she returns 5 books, she checks out 5 books. If she returns 9 books, she checks out 9 books. If she returns all 12 books, she always checks out 12 more books. Create an equation in y=mx+b format and graph it.

This graph is a horizontal line where y=12.

Amahle loves her shoes and currently has 5 pairs. She does not have room for more than 5 pairs, so each time she purchases more shoes, she gives that number of pairs to her little sister. Create an equation in y=mx+b format and graph it.

The graph is a horizontal line where y=5

Harry volunteers at an organization concerned with reforestation. He helps to replace trees brought down by storms at a 1:1 ratio. Any trees destroyed, whether the number of trees is 100, 250, or even 500, are replaced to maintain the current number of 500 trees. Create an equation in y=mx+b format and graph it.

This graph is a horizontal line where y=500.

Myrtle loves to make quilts and also enjoys keeping eight favorite ones for herself at all times. For example, if she makes five quilts, she sells all five of them, but occasionally, she’ll keep one that she made and donate one in its place so that she always keeps her eight favorite ones. Create an equation in y=mx+b format and graph it.

The resulting graph is a horizontal line where y=8.

Fynn enjoys collecting stamps. He has a display box that will hold 50 stamps, so any time he is given a new stamp(s), he checks his collection to see whether he wants to replace one or if he is going to sell the stamp online so that he always has exactly 50 stamps. Create an equation in y=mx+b format and graph it.

The resulting graph is a horizontal line where y=50.

Erica has had a summer job for the last four summers and she spends what she has from the summer on Christmas presents. She made $500 the first year and she was able to save $250. The next year, she made $750 and her expenses were $500, leaving her with $250. After making $1000 the third year and discovering that her expenses were $750, Erica wondered what she was doing wrong. Create an equation in y=mx+b format and graph it.

The graph is a horizontal line where y=250.

Mateo made a goal to finish all homework each day so that he wouldn’t have any assignments rolling over to the next day. He accomplished his goal for the last five days, even when he was assigned up to 7 assignments daily. Create an equation in y=mx+b format and graph it.

The graph is a horizontal line where y=0.

Bonus! One week near the end of the school year, Mateo decided he did not want to do any homework. Unfortunately, he was assigned 7 homework assignments each of the five days. Graph the resulting slope. Hint: This one is a positive slope and not a horizontal line.

The graph for this one is y=7x with a positive slope crossing the y-axis at 0.

Sally has a doll collection with 15 dolls. Her mom says they don’t have room for more than 15 dolls. If Sally gets one new doll, she donates one doll from her collection to a local charity. If Sally gets two new dolls, she donates two dolls from her collection to a local charity. If she gets three new dolls, she donates three dolls to a local charity, etc. so that she always has 15 dolls. Create an equation in y=mx+b format and graph it.

The graph is a horizontal line where y=15.

Bonus! Sally found a special collection of 6 dolls and asked her mom if she could increase her total collection number to 6. Her mom replied, “I’ll compromise with you. I would prefer a maximum of 20 dolls while you prefer a maximum of 26 dolls. I’ll meet you at the mean of those numbers if you can tell me how many dolls you’ll need to donate if you get get the six new dolls. Graph the resulting compromise. How many dolls would Sally need to donate if she agrees to the compromise suggested by her mom?

The linear equation is y=23. Sally would need to donate 3 dolls per the compromise.

Possible counter offers might include: Sally’s mom might say that she wants to stay with the original limit of 20. y=20 (already graphed). Sally’s mom might agree to increasing the limit to 26. y=26 (horizontal line at y=26). Sally’s mom might agree to increasing the number of dolls based on a variable. For example, she might say that Sally can earn up up to six extra dolls by volunteering in a community service project in which she could earn one doll for each hour of community service she provides. Below is the slope of how the number of dolls would increase based on the variable. y=1(x)+20.

Find more resources at StudentSurvive2Thrive.blogspot.com

Student Survive 2 Thrive

Saturday, May 28, 2022

Horizontal Linear Equations and Graphs Including Real Life Examples

No comments:

Post a Comment