Student Survive 2 Thrive: May 2022

Sunday, May 29, 2022

Pythagorean Theorem Practice Test - Free Math Resource!

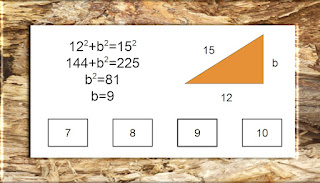
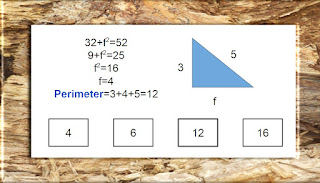
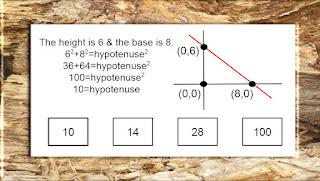
This free resource offers a practice test featuring the Pythagorean Theorem. It includes 15 questions ranging from simple to more complex questions. This practice test is created in adaptive mode so that you can check your answers immediately after each question. If you aren't familiar with this theorem or would like to review information related to it, you may wish to visit Khan Academy's Pythagorean Theorem video.

Directions

Click on the first graphic to enlarge to full screen.
Record your answers on a piece of paper.
Click on the graphic or the next thumbnail at the bottom of the screen.
Check your answers.

Thank you very much for visiting my Student Survive 2 Thrive blog! If you would like to see more of my resources, you have several options: click on my site map, go to the topics options, or type your desired topic into my search bar. Below are a few additional math resources that I have created:

Created by Katrena - All rights reserved

What is the value for c? The two legs of the right triangle measure 3 and 4. Choices are 2, 3, 4, or 5.

c=5 (Use the Pythagorean Theorem to determine this answer by using a squared + b squared = c squared.)

What is the value for x? Right triangle legs are 6 and 8. Choices are: 9, 10, 12, and 15.

x=10 (Use the Pythagorean Theorem in which a squared + b squared = c squared).

What is the value for b? Right triangle leg is 12 and the hypotenuse is 15. Choices are: 7, 8, 9, and 10

What is the value for p? Right triangle leg is 4 and the hypotenuse is 5. Choices are: 3, 6, 8, and 10.

What is the perimeter of the triangle? Right triangle has a leg of 3 and hypotenuse of 5 and an unknown variable for the other leg. Choices are: 4, 6, 12, and 16.

The perimeter equals 12. Use the Pythagorean Theorem to determine the missing variable and then add all sides.

What is the perimeter of the triangle? Right triangle pictured: one leg is 9 and the hypotenuse is 15. Choices are: 6, 12, 24, and 36.

The perimeter is 36. Use the Pythagorean Theorem to determine the missing leg and then add all 3 sides.

What is the perimeter of the rectangle? Picture includes a rectangle with a height of 3. A line is drawn diagonally from the top right to the bottom left of the rectangle and that has a length of 5. The base has an unknown variable. Choices are: 4, 12, 14, and 19.

The perimeter of the rectangle is 14. Use the Pythagorean Theorem to determine the base. Add all four numbers on the rectangle to get the perimeter.

What is the area of the triangle? Right triangle pictured with a leg of 8 and hypotenuse of 10 with an unknown variable for the other leg. Choices are: 24, 48, 28, and 6.

The area of the triangle is 24. Use the Pythagorean Theorem to determine the height. Area of a triangle = 1/2 base times the height.

What is the perimeter of the square? Pictured is a square with an unknown variable for the width and height. A line extends across the square from top left to bottom right with a length of the square root of 18. Choices are: 81, 72, 36, and 12.

The perimeter of the square is 12. Use the Pythagorean Theorem to determine that all sides of the square equal 3. Add all four sides to get 12.

What is the area of the square? A square is pictured with unknown variables for the height and width. A line extends from the top left corner to the bottom right corner with a length of the square root of 50. Choices are: 12.5, 20, 25, 625.

Area of the square is 25. Use the Pythagorean Theorem to determine that the sides of the square equal 5. Multiply the height and width to determine the area of a square.

What is the length of the hypotenuse? Pictured is a right triangle with the following coordinates: (0,6), (0,0), and (8,0). Choices are 10, 14, 28, and 100.

The length of the hypotenuse is 10. Use the Pythagorean Theorem to determine that the two legs are 6 and 8 with a resulting hypotenuse of 10.

What are the coordinates for k? A pictured graph has 3 triangle coordinates. K is above l and is unknown. L has coordinates of (0,0). M has coordinates of (8,0). Choices are: (0,10), (6,0), (12,0), (0,6).

The missing coordinates are (0,6). Use the Pythagorean Theorem to determine that the missing side has a height of 6.

What is the area of the triangle? Pictured is a graph forming a right triangle with the following coordinates: (0,12), (0,0), and (16,0). Choices are: 20, 96, 120, and 192).

The area of the triangle is 96. The base is 16 and the height is 12. Area of a triangle equals 1/2 base times the height.

Michael marked points on a graph at (8,0) and (0,6). He then drew a line through them, forming a triangle with the origin. What is the perimeter of the resulting triangle? Choices are: 24, 48, 60, and 68.

The perimeter of the triangle is 24. Use the Pythagorean Theorem to determine legs of 8 and 6 and a hypotenuse of 10.

Carlotta graphed a straight line using a linear equation of y= -4/3x+4. The line created a triangle with the point where the x- and y-axes cross over. What is the perimeter of the resulting triangle? Choices are: 5, 6, 12, and 24.

The perimeter of the triangle is 12. Use the Pythagorean Theorem to determine 2 legs of 4 and 3 with a hypoteneuse of 5. Add the 3 sides to get the perimeter.

Find more resources at StudentSurvive2Thrive.blogspot.com

Saturday, May 28, 2022

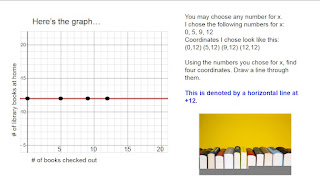
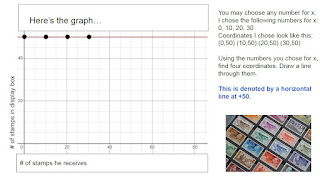
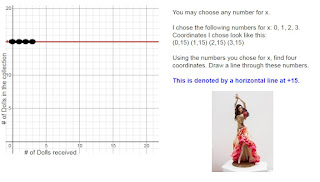
Horizontal Linear Equations and Graphs Including Real Life Examples

This free math practice test includes examples from real life that would result in graphing points that when drawing through them would create a horizontal line. I created this practice test in adaptive mode so that you can the correct answers on the next slide along with a detailed explanation.

Directions

Click on the first graphic below.
Write your answers on paper and graph your answers on graph paper.
Click on the graphic or on the next thumbnail at the bottom of the screen to advance to the next slide.
Check your answers and review the detailed feedback if needed.
Repeat the above steps if you wish to review the information again.

Note: In an effort to create a resource that includes real life examples, it is helpful to understand that the real life examples would in reality be specific points on a graph and would not equate to a line that would include all values for y between the numbers given. However, for the purposes of practicing this level of math, the linear equations would result from a line drawn that would connect and continue beyond these points.

I hope you enjoy my free resources on Student Survive 2 Thrive. If you wish to find more resources, you have several options: go to my site map, go to your desired topic such as math, or type your desired topic in my search bar. I've also included some related math practice tests below:

Horizontal Linear Equations & Graphs Free Practice Test

Larry is at an Easter egg hunt. He currently has 7 eggs in his basket. Every time he bends over to pick up an egg, he drops the same number of eggs. When he picks up 2 eggs, he drops 2 eggs. When he picks up 3 eggs, he drops 3 eggs. The same thing happens when he picks up four eggs. Larry is frustrated when he sees that he only has 7 eggs at the end of the hunt! Create an equation in y=mx+b format and graph the equation.

The resulting graph is a horizontal line where y=7.

Chia-Hao has a toy collection with 20 toys. His dad said he can keep collecting toys, but for every toy he adds to his collection, he will have to donate or sell the same number of toys. If he adds 5, 10, or even 15 toys, Chia-Hao will donate the same number of toys. Write the equation using y=mx+b format and graph it.

The graph is a horizontal line where y=20

Zuzanna loves to go to the library. She always makes sure that she has 12 books at home to read. If she returns 5 books, she checks out 5 books. If she returns 9 books, she checks out 9 books. If she returns all 12 books, she always checks out 12 more books. Create an equation in y=mx+b format and graph it.

This graph is a horizontal line where y=12.

Amahle loves her shoes and currently has 5 pairs. She does not have room for more than 5 pairs, so each time she purchases more shoes, she gives that number of pairs to her little sister. Create an equation in y=mx+b format and graph it.

The graph is a horizontal line where y=5

Harry volunteers at an organization concerned with reforestation. He helps to replace trees brought down by storms at a 1:1 ratio. Any trees destroyed, whether the number of trees is 100, 250, or even 500, are replaced to maintain the current number of 500 trees. Create an equation in y=mx+b format and graph it.

This graph is a horizontal line where y=500.

Myrtle loves to make quilts and also enjoys keeping eight favorite ones for herself at all times. For example, if she makes five quilts, she sells all five of them, but occasionally, she’ll keep one that she made and donate one in its place so that she always keeps her eight favorite ones. Create an equation in y=mx+b format and graph it.

The resulting graph is a horizontal line where y=8.

Fynn enjoys collecting stamps. He has a display box that will hold 50 stamps, so any time he is given a new stamp(s), he checks his collection to see whether he wants to replace one or if he is going to sell the stamp online so that he always has exactly 50 stamps. Create an equation in y=mx+b format and graph it.

The resulting graph is a horizontal line where y=50.

Erica has had a summer job for the last four summers and she spends what she has from the summer on Christmas presents. She made $500 the first year and she was able to save $250. The next year, she made $750 and her expenses were $500, leaving her with $250. After making $1000 the third year and discovering that her expenses were $750, Erica wondered what she was doing wrong. Create an equation in y=mx+b format and graph it.

The graph is a horizontal line where y=250.

Mateo made a goal to finish all homework each day so that he wouldn’t have any assignments rolling over to the next day. He accomplished his goal for the last five days, even when he was assigned up to 7 assignments daily. Create an equation in y=mx+b format and graph it.

The graph is a horizontal line where y=0.

Bonus! One week near the end of the school year, Mateo decided he did not want to do any homework. Unfortunately, he was assigned 7 homework assignments each of the five days. Graph the resulting slope. Hint: This one is a positive slope and not a horizontal line.

The graph for this one is y=7x with a positive slope crossing the y-axis at 0.

Sally has a doll collection with 15 dolls. Her mom says they don’t have room for more than 15 dolls. If Sally gets one new doll, she donates one doll from her collection to a local charity. If Sally gets two new dolls, she donates two dolls from her collection to a local charity. If she gets three new dolls, she donates three dolls to a local charity, etc. so that she always has 15 dolls. Create an equation in y=mx+b format and graph it.

The graph is a horizontal line where y=15.

Bonus! Sally found a special collection of 6 dolls and asked her mom if she could increase her total collection number to 6. Her mom replied, “I’ll compromise with you. I would prefer a maximum of 20 dolls while you prefer a maximum of 26 dolls. I’ll meet you at the mean of those numbers if you can tell me how many dolls you’ll need to donate if you get get the six new dolls. Graph the resulting compromise. How many dolls would Sally need to donate if she agrees to the compromise suggested by her mom?

The linear equation is y=23. Sally would need to donate 3 dolls per the compromise.

Possible counter offers might include: Sally’s mom might say that she wants to stay with the original limit of 20. y=20 (already graphed). Sally’s mom might agree to increasing the limit to 26. y=26 (horizontal line at y=26). Sally’s mom might agree to increasing the number of dolls based on a variable. For example, she might say that Sally can earn up up to six extra dolls by volunteering in a community service project in which she could earn one doll for each hour of community service she provides. Below is the slope of how the number of dolls would increase based on the variable. y=1(x)+20.